【笔记】动态规划-求解资源分配问题|Hello World

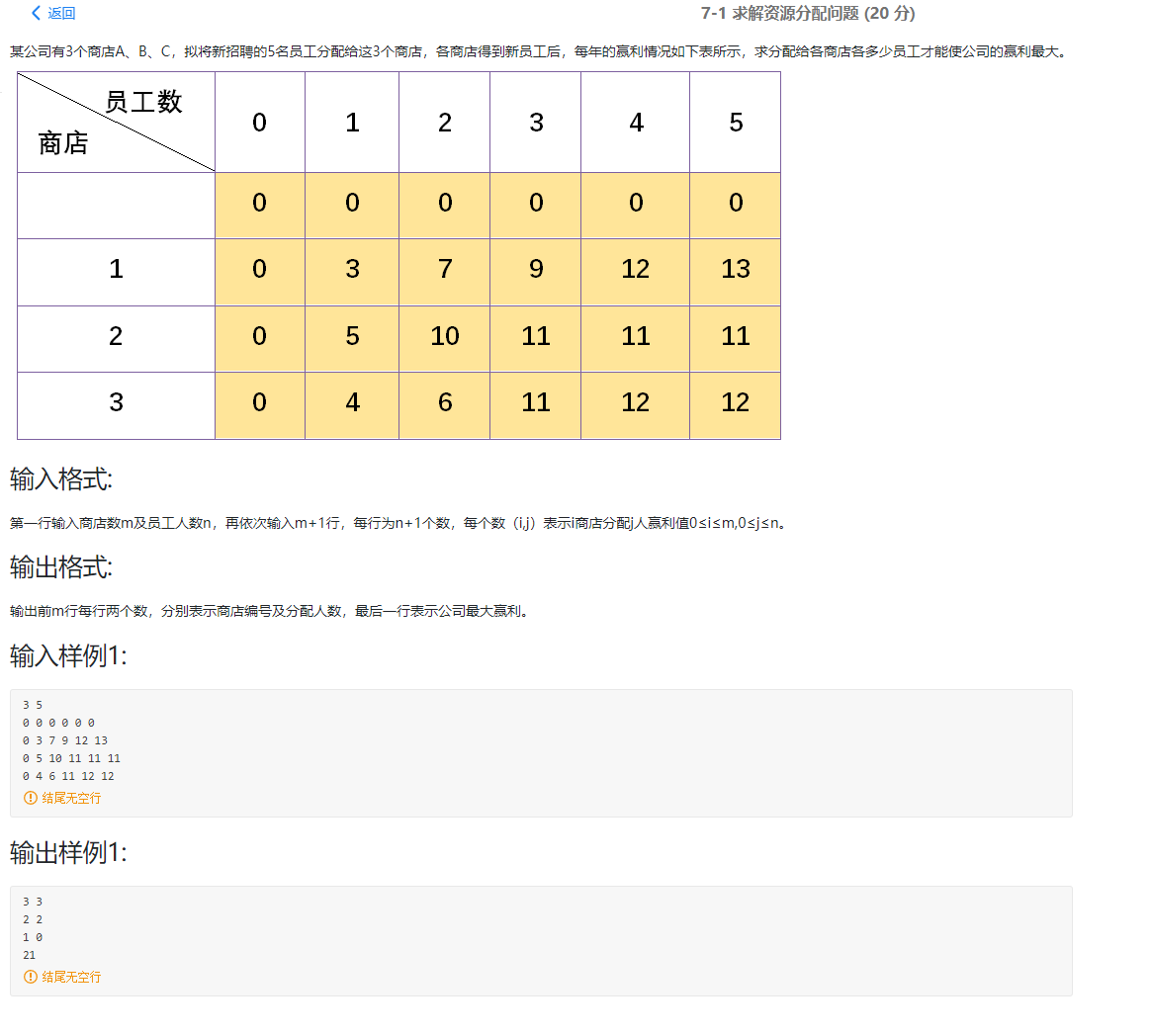
1. 题目

2. 思路

分析题目，可以知道第 i 个商店有 n 个员工时候的收益，所以可以把问题分解为
前 i 个商店分配 n 个员工的最大收益 = 第 i 个商店分配 k 个员工的收益 + 前 i - 1 个商店分配 n - k 个员工的收益的最大值
所以 状态转移方程 就是

dp[i][n] = max(dp[i][n], arr[i][k] + dp[i-1][n-k])

3. 代码

#include <bits/stdc++.h>

using namespace std;
#define Max_N 101
int m, n;
int arr[Max_N][Max_N];
int res[Max_N][Max_N];
int dp[Max_N][Max_N];//前 i 个商店 n 个人的最大收益 dp[i][n]=dp[i-1][n-k]+dp[i][k]
int run() {
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j <= n; ++j) {
            // 前 i 个商店 分配 n 个员工的情况下，进行拆分，遍历
            for (int k = 1; k <= j; ++k) {
                int sum = dp[i - 1][j - k] + arr[i][k];
                if (sum >= dp[i][j]) {
                    dp[i][j] = sum;
                    // res 是存储结果的，前 i 个商店分配 n 个员工的情况下，第 i 个商店分配了 k 个人
                    res[i][j] = k;
                }
            }
        }
    }
    return dp[m][n];
}

int main() {
    cin >> m >> n;
    for (int i = 0; i <= m; ++i) {
        for (int j = 0; j <= n; ++j) {
            cin >> arr[i][j];
        }
    }

    int sum = run();
    // 输出分配详情，最开始肯定是第m个商店分配了n个人
    for (int i = m; i > 0; --i) {
        cout << i << " " << res[i][n] << endl;
        //把分配的人减去，n 就变成了前 i - 1 个商店分配的人数了
        n -= res[i][n];
    }
    cout << sum;
    return 0;
}